Pallas 快速入门

Pallas 快速入门#

Pallas 是 JAX 的一个扩展，它支持为 GPU 和 TPU 编写自定义内核。Pallas 允许您使用相同的 JAX 函数和 API，但在一个较低的抽象级别上运行。

具体来说，Pallas 要求用户考虑内存访问以及如何在硬件加速器中的多个计算单元之间分配计算。在 GPU 上，Pallas 会降级到 Triton，而在 TPU 上，Pallas 会降级到 Mosaic。

让我们深入研究一些示例。

注意：Pallas 仍然是一个实验性 API，您可能会因为更改而中断！

Pallas 中的 Hello world#

from functools import partial

import jax
from jax.experimental import pallas as pl
import jax.numpy as jnp
import numpy as np

我们首先用 Pallas 编写 “hello world”，一个添加两个向量的内核。

def add_vectors_kernel(x_ref, y_ref, o_ref):
  x, y = x_ref[...], y_ref[...]
  o_ref[...] = x + y

Ref 类型

让我们稍微剖析一下这个函数。与你可能编写的大多数 JAX 函数不同，它不接受 jax.Array 作为输入，也不返回任何值。相反，它接受 Ref 对象作为输入，这些对象表示内存中的可变缓冲区。请注意，我们也没有任何输出，但我们得到了一个 o_ref，它对应于期望的输出。

从 Ref 读取

在主体中，我们首先从 x_ref 和 y_ref 读取，用 [...] 表示（省略号表示我们正在读取整个 Ref；或者我们也可以使用 x_ref[:]）。像这样从 Ref 读取会返回一个 jax.Array。

写入 Ref

然后我们将 x + y 写入 o_ref。JAX 历史上不支持突变——jax.Array 是不可变的！Ref 是新的（实验性的）类型，允许在特定情况下进行突变。我们可以将写入 Ref 解释为突变其底层缓冲区。

因此，我们编写了一个我们称之为“内核”的东西，我们将其定义为一个程序，该程序将在加速器上作为原子执行单元运行，而无需与主机进行任何交互。我们如何从 JAX 计算中调用它？我们使用 pallas_call 高阶函数。

@jax.jit
def add_vectors(x: jax.Array, y: jax.Array) -> jax.Array:
  return pl.pallas_call(
      add_vectors_kernel,
      out_shape=jax.ShapeDtypeStruct(x.shape, x.dtype)
  )(x, y)
add_vectors(jnp.arange(8), jnp.arange(8))

Array([ 0,  2,  4,  6,  8, 10, 12, 14], dtype=int32)

pallas_call 将 Pallas 内核函数提升为一个可以作为更大的 JAX 程序的一部分调用的操作。但是，要做到这一点，它还需要一些更多的细节。在这里，我们指定 out_shape，一个具有 .shape 和 .dtype 的对象（或它们的列表）。out_shape 决定了我们的 add_vector_kernel 中 o_ref 的形状/dtype。

pallas_call 返回一个接收并返回 jax.Array 的函数。

这里实际发生了什么？

到目前为止，我们已经描述了如何思考 Pallas 内核，但我们实际完成的是我们正在编写一个非常接近计算单元执行的函数，因为值被加载到内存层次结构的最内部（最快）部分。

在 GPU 上，x_ref 对应于高带宽内存 (HBM) 中的一个值，当我们执行 x_ref[...] 时，我们将值从 HBM 复制到静态 RAM (SRAM)（一般来说，这是一个代价很高的操作！）。然后，我们使用 GPU 向量计算来执行加法，然后将 SRAM 中的结果值复制回 HBM。

在 TPU 上，我们做的事情略有不同。在内核执行之前，我们将值从 HBM 获取到 SRAM。x_ref 因此对应于 SRAM 中的一个值，当我们执行 x_ref[...] 时，我们将该值从 SRAM 复制到寄存器中。然后，我们使用 TPU 向量计算来执行加法，然后将结果值复制回 SRAM。内核执行后，SRAM 值被复制回 HBM。

我们正在编写特定于后端的 Pallas 指南。即将推出！

Pallas 编程模型#

在我们的“Hello World”示例中，我们编写了一个非常简单的内核。它利用了我们的 8 大小的数组可以舒适地容纳在硬件加速器的 SRAM 中的事实。在大多数实际应用中，情况并非如此！

编写 Pallas 内核的一部分是思考如何获取驻留在高带宽内存（HBM，也称为 DRAM）中的大型数组，并表达对可以容纳在 SRAM 中的那些数组的“块”进行操作的计算。

网格示例#

要自动“分割”输入和输出，你需要向 pallas_call 提供一个 grid 和 BlockSpec。

grid 是一个整数元组（例如 ()、(2, 3, 4) 或 (8,)），它指定了一个迭代空间。例如，网格 (4, 5) 将有 20 个元素：(0, 0), (0, 1), ..., (0, 4), (1, 0), ..., (3, 4)。我们为每个元素运行一次内核函数，这是一种单程序多数据 (SPMD) 编程风格。

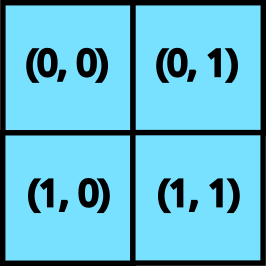
A visualization of a 2D grid

2D 网格

当我们向 pallas_call 提供 grid 时，内核将执行 prod(grid) 次。这些调用的每一次都被称为“程序”。要访问内核当前正在执行哪个程序（即网格的哪个元素），我们使用 program_id(axis=...)。例如，对于调用 (1, 2)，program_id(axis=0) 返回 1，program_id(axis=1) 返回 2。

这是一个使用 grid 和 program_id 的示例内核。

def iota_kernel(o_ref):
  i = pl.program_id(0)
  o_ref[i] = i

我们现在使用带有附加 grid 参数的 pallas_call 执行它。在 GPU 上，我们可以直接像这样调用内核

# GPU version
def iota(size: int):
  return pl.pallas_call(iota_kernel,
                        out_shape=jax.ShapeDtypeStruct((size,), jnp.int32),
                        grid=(size,))()
iota(8)

Array([0, 1, 2, 3, 4, 5, 6, 7], dtype=int32)

TPU 区分向量和标量内存空间，在这种情况下，输出必须放置在标量内存 (TPUMemorySpace.SMEM) 中，因为 i 是一个标量。有关更多详细信息，请阅读 TPU 及其内存空间。要在 TPU 上调用上述内核，请运行

# TPU version
from jax.experimental.pallas import tpu as pltpu

def iota(size: int):
  return pl.pallas_call(iota_kernel,
                        out_specs=pl.BlockSpec(memory_space=pltpu.TPUMemorySpace.SMEM),
                        out_shape=jax.ShapeDtypeStruct((size,), jnp.int32),
                        grid=(size,))()
iota(8)

网格语义#

在 GPU 上，每个程序在单独的线程上并行执行。因此，我们需要考虑写入 HBM 的竞争条件。一种合理的方法是以这样一种方式编写我们的内核，即不同的程序写入 HBM 中不相交的位置，以避免这些并行写入。另一方面，并行化计算是我们如何快速执行矩阵乘法等操作的方法。

相比之下，TPU 的运行方式类似于非常宽的 SIMD 机器。一些 TPU 模型包含多个内核，但在许多情况下，TPU 可以被视为单线程处理器。TPU 上的网格可以指定为并行和顺序维度的组合，其中顺序维度保证按顺序运行。

你可以在网格，又名循环中的内核和值得注意的属性和限制中阅读更多详细信息。

块规范示例#

考虑到 grid 和 program_id，Pallas 提供了一个抽象，可以处理在许多内核中看到的一些常见索引模式。为了建立直觉，让我们尝试实现一个矩阵乘法。

在 Pallas 中实现矩阵乘法的一个简单策略是递归地实现它。我们知道我们的底层硬件支持小的矩阵乘法（使用 GPU 和 TPU 张量核），所以我们只是用较小的矩阵乘法来表示大的矩阵乘法。

假设我们有输入矩阵 \(X\) 和 \(Y\)，并且正在计算 \(Z = XY\)。我们首先将 \(X\) 和 \(Y\) 表示为分块矩阵。\(X\) 将具有“行”块，\(Y\) 将具有“列”块。

\[\begin{split} \begin{align*} X = \begin{bmatrix} X_0 \\ X_1 \end{bmatrix} \end{align*} \end{split}\]

\[ \begin{align*} Y = \begin{bmatrix} Y_0 & Y_1 \end{bmatrix} \end{align*} \]

\[\begin{split} \begin{align*} Z &= \begin{bmatrix} X_0 \\ X_1 \end{bmatrix} \begin{matrix} \begin{bmatrix} Y_0 & Y_1 \end{bmatrix} \\ ~ \end{matrix} \\ &= \begin{bmatrix} X_0 Y_0 & X_0 Y_1 \\ X_1 Y_0 & X_1 Y_1 \end{bmatrix} \end{align*} \end{split}\]

我们的策略是，因为 \(Z\) 也是一个分块矩阵，我们可以将 Pallas 内核中的每个程序分配给其中一个输出块。计算每个输出块对应于在 \(X\) 的“行”块和 \(Y\) 的“列”块之间进行较小的矩阵乘法。

为了表达这种模式，我们使用 BlockSpec。一个 BlockSpec 为每个输入和输出指定一个块形状，以及一个“索引映射”函数，该函数将一组程序索引映射到一个块索引。

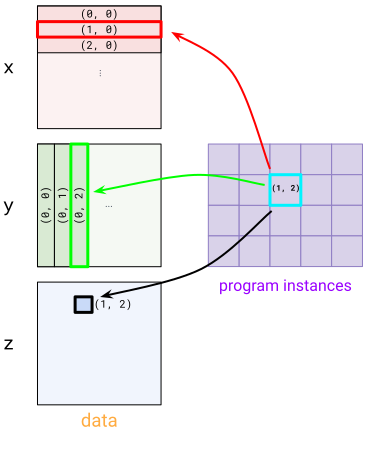
A visualization of a BlockSpec`

BlockSpec 的可视化

举个具体的例子，假设我们想将两个 (1024, 1024) 矩阵 x 和 y 相乘，生成 z，并且想以 4 种方式并行化计算。我们将 z 分成 4 个 (512, 512) 的块，其中每个块都使用 (512, 1024) x (1024, 512) 矩阵乘法计算。为了表达这一点，我们首先使用 (2, 2) 网格（每个程序一个块）。

对于 x，我们使用 BlockSpec((512, 1024), lambda i, j: (i, 0)) – 这会将 x 分割成“行”块。要理解这一点，请看程序实例 (1, 0) 和 (1, 1) 如何在 x 中选择 (1, 0) 块。对于 y，我们使用转置版本 BlockSpec((1024, 512), lambda i, j: (0, j))。最后，对于 z，我们使用 BlockSpec((512, 512), lambda i, j: (i, j))。

这些 BlockSpec 通过 in_specs 和 out_specs 传递给 pallas_call。

有关 BlockSpec 的更多详细信息，请参阅 BlockSpec，即如何分割输入。

在底层，pallas_call 会自动将您的输入和输出分割成传递给内核的每个块的 Ref。

def matmul_kernel(x_ref, y_ref, z_ref):
  z_ref[...] = x_ref[...] @ y_ref[...]

def matmul(x: jax.Array, y: jax.Array):
  return pl.pallas_call(
    matmul_kernel,
    out_shape=jax.ShapeDtypeStruct((x.shape[0], y.shape[1]), x.dtype),
    grid=(2, 2),
    in_specs=[
        pl.BlockSpec((x.shape[0] // 2, x.shape[1]), lambda i, j: (i, 0)),
        pl.BlockSpec((y.shape[0], y.shape[1] // 2), lambda i, j: (0, j))
    ],
    out_specs=pl.BlockSpec(
        (x.shape[0] // 2, y.shape[1] // 2), lambda i, j: (i, j),
    )
  )(x, y)
k1, k2 = jax.random.split(jax.random.key(0))
x = jax.random.normal(k1, (1024, 1024))
y = jax.random.normal(k2, (1024, 1024))
z = matmul(x, y)
np.testing.assert_allclose(z, x @ y)

请注意，这只是一个非常简单的矩阵乘法实现，但可以将其视为各种优化类型的起点。让我们为矩阵乘法添加一个额外的特性：融合激活。这实际上非常容易！只需将高阶激活函数传递到内核中即可。

def matmul_kernel(x_ref, y_ref, z_ref, *, activation):
  z_ref[...] = activation(x_ref[...] @ y_ref[...])

def matmul(x: jax.Array, y: jax.Array, *, activation):
  return pl.pallas_call(
    partial(matmul_kernel, activation=activation),
    out_shape=jax.ShapeDtypeStruct((x.shape[0], y.shape[1]), x.dtype),
    grid=(2, 2),
    in_specs=[
        pl.BlockSpec((x.shape[0] // 2, x.shape[1]), lambda i, j: (i, 0)),
        pl.BlockSpec((y.shape[0], y.shape[1] // 2), lambda i, j: (0, j))
    ],
    out_specs=pl.BlockSpec(
        (x.shape[0] // 2, y.shape[1] // 2), lambda i, j: (i, j)
    ),
  )(x, y)
k1, k2 = jax.random.split(jax.random.key(0))
x = jax.random.normal(k1, (1024, 1024))
y = jax.random.normal(k2, (1024, 1024))
z = matmul(x, y, activation=jax.nn.relu)
np.testing.assert_allclose(z, jax.nn.relu(x @ y))

最后，让我们强调 Pallas 的一个很酷的特性：它可以与 jax.vmap 组合！要将此矩阵乘法转换为批处理版本，我们只需要 vmap 它即可。

k1, k2 = jax.random.split(jax.random.key(0))
x = jax.random.normal(k1, (4, 1024, 1024))
y = jax.random.normal(k2, (4, 1024, 1024))
z = jax.vmap(partial(matmul, activation=jax.nn.relu))(x, y)
np.testing.assert_allclose(z, jax.nn.relu(jax.vmap(jnp.matmul)(x, y)))