高级自动微分

在本教程中，您将了解 JAX 中自动微分（autodiff）的复杂应用，并更好地理解在 JAX 中进行求导既简单又强大。

如果您还没有，请务必查看 自动微分 教程，以了解 JAX autodiff 的基础知识。

设置

import jax
import jax.numpy as jnp
from jax import grad, jit, vmap
from jax import random

key = random.key(0)

求梯度（第 2 部分）

高阶导数

JAX 的 autodiff 使得计算高阶导数变得容易，因为计算导数的函数本身也是可微的。因此，高阶导数与堆叠变换一样简单。

单变量情况已在 自动微分 教程中介绍，该示例展示了如何使用 jax.grad() 计算 \(f(x) = x^3 + 2x^2 - 3x + 1\) 的导数。

在多变量情况下，高阶导数更加复杂。函数的二阶导数由其 Hessian 矩阵 表示，定义如下：

\[(\mathbf{H}f)_{i,j} = \frac{\partial^2 f}{\partial_i\partial_j}.\]

多个变量的实值函数 \(f: \mathbb R^n\to\mathbb R\) 的 Hessian 可以识别为其梯度的 雅可比。

JAX 提供了两种变换来计算函数的雅可比矩阵，jax.jacfwd() 和 jax.jacrev()，分别对应前向和逆向模式自动微分。它们给出相同的答案，但一种方法在不同的情况下可能比另一种方法更有效 - 请参考 关于自动微分的视频。

def hessian(f):
  return jax.jacfwd(jax.grad(f))

让我们检查一下在点积 \(f: \mathbf{x} \mapsto \mathbf{x} ^\top \mathbf{x}\) 上是否正确。

如果 \(i=j\)，\(\frac{\partial^2 f}{\partial_i\partial_j}(\mathbf{x}) = 2\)。否则，\(\frac{\partial^2 f}{\partial_i\partial_j}(\mathbf{x}) = 0\)。

def f(x):
  return jnp.dot(x, x)

hessian(f)(jnp.array([1., 2., 3.]))

Array([[2., 0., 0.],
       [0., 2., 0.],
       [0., 0., 2.]], dtype=float32)

高阶优化

一些元学习技术，如模型无关元学习 (MAML)，需要对梯度更新进行微分。在其他框架中，这可能非常繁琐，但在 JAX 中，这要容易得多

def meta_loss_fn(params, data):
  """Computes the loss after one step of SGD."""
  grads = jax.grad(loss_fn)(params, data)
  return loss_fn(params - lr * grads, data)

meta_grads = jax.grad(meta_loss_fn)(params, data)

停止梯度

Autodiff 能够自动计算函数相对于其输入的梯度。但是，有时您可能想要一些额外的控制：例如，您可能想要避免反向传播通过计算图的某些子集的梯度。

例如，考虑 TD(0) (时序差分) 强化学习更新。它用于从与环境交互的经验中学习估计环境中状态的值。假设状态 \(s_{t-1}\) 中的值估计 \(v_{\theta}(s_{t-1}\)) 由线性函数参数化。

# Value function and initial parameters
value_fn = lambda theta, state: jnp.dot(theta, state)
theta = jnp.array([0.1, -0.1, 0.])

考虑从状态 \(s_{t-1}\) 到状态 \(s_t\) 的转换，在此期间您观察到奖励 \(r_t\)

# An example transition.
s_tm1 = jnp.array([1., 2., -1.])
r_t = jnp.array(1.)
s_t = jnp.array([2., 1., 0.])

网络参数的 TD(0) 更新为

\[ \Delta \theta = (r_t + v_{\theta}(s_t) - v_{\theta}(s_{t-1})) \nabla v_{\theta}(s_{t-1}) \]

此更新不是任何损失函数的梯度。

但是，它可以写为伪损失函数的梯度

\[ L(\theta) = - \frac{1}{2} [r_t + v_{\theta}(s_t) - v_{\theta}(s_{t-1})]^2 \]

如果目标 \(r_t + v_{\theta}(s_t)\) 对参数 \(\theta\) 的依赖关系被忽略。

您如何在 JAX 中实现这一点？如果您天真地编写伪损失，您会得到

def td_loss(theta, s_tm1, r_t, s_t):
  v_tm1 = value_fn(theta, s_tm1)
  target = r_t + value_fn(theta, s_t)
  return -0.5 * ((target - v_tm1) ** 2)

td_update = jax.grad(td_loss)
delta_theta = td_update(theta, s_tm1, r_t, s_t)

delta_theta

Array([-1.2,  1.2, -1.2], dtype=float32)

但是 td_update 将不会计算 TD(0) 更新，因为梯度计算将包括 target 对 \(\theta\) 的依赖关系。

您可以使用 jax.lax.stop_gradient() 强制 JAX 忽略目标对 \(\theta\) 的依赖关系

def td_loss(theta, s_tm1, r_t, s_t):
  v_tm1 = value_fn(theta, s_tm1)
  target = r_t + value_fn(theta, s_t)
  return -0.5 * ((jax.lax.stop_gradient(target) - v_tm1) ** 2)

td_update = jax.grad(td_loss)
delta_theta = td_update(theta, s_tm1, r_t, s_t)

delta_theta

Array([ 1.2,  2.4, -1.2], dtype=float32)

这将把 target 视为不依赖于参数 \(\theta\) 并计算对参数的正确更新。

现在，让我们也使用原始 TD(0) 更新表达式来计算 \(\Delta \theta\)，以交叉检查我们的工作。您可能希望尝试使用 jax.grad() 和您目前的知识来自己实现这一点。以下是我们的解决方案

s_grad = jax.grad(value_fn)(theta, s_tm1)
delta_theta_original_calculation = (r_t + value_fn(theta, s_t) - value_fn(theta, s_tm1)) * s_grad

delta_theta_original_calculation # [1.2, 2.4, -1.2], same as `delta_theta`

Array([ 1.2,  2.4, -1.2], dtype=float32)

jax.lax.stop_gradient 也可以在其他设置中使用，例如，如果您希望来自某个损失的梯度仅影响神经网络的某些参数（因为，例如，其他参数使用不同的损失进行训练）。

使用 stop_gradient 的直通估计器

直通估计器是一种技巧，用于定义否则不可微函数的“梯度”。给定一个用作我们希望找到梯度的较大函数的一部分的不可微函数 \(f : \mathbb{R}^n \to \mathbb{R}^n\)，我们在反向传播期间简单地假装 \(f\) 是恒等函数。这可以使用 jax.lax.stop_gradient 巧妙地实现

def f(x):
  return jnp.round(x)  # non-differentiable

def straight_through_f(x):
  # Create an exactly-zero expression with Sterbenz lemma that has
  # an exactly-one gradient.
  zero = x - jax.lax.stop_gradient(x)
  return zero + jax.lax.stop_gradient(f(x))

print("f(x): ", f(3.2))
print("straight_through_f(x):", straight_through_f(3.2))

print("grad(f)(x):", jax.grad(f)(3.2))
print("grad(straight_through_f)(x):", jax.grad(straight_through_f)(3.2))

f(x):  3.0
straight_through_f(x): 3.0
grad(f)(x): 0.0
grad(straight_through_f)(x): 1.0

每个示例的梯度

虽然大多数 ML 系统出于计算效率和/或方差减少的原因从数据批次中计算梯度和更新，但有时需要访问与批次中每个特定样本相关的梯度/更新。

例如，这需要根据梯度幅度对数据进行优先级排序，或者对每个样本进行剪切/归一化。

在许多框架（PyTorch、TF、Theano）中，计算每个示例的梯度通常并不容易，因为库直接累积批次上的梯度。朴素的解决方法，例如为每个示例计算单独的损失，然后聚合生成的梯度，通常效率非常低。

在 JAX 中，您可以以一种简单而高效的方式定义计算每个样本梯度的代码。

只需将 jax.jit()、jax.vmap() 和 jax.grad() 变换组合在一起

perex_grads = jax.jit(jax.vmap(jax.grad(td_loss), in_axes=(None, 0, 0, 0)))

# Test it:
batched_s_tm1 = jnp.stack([s_tm1, s_tm1])
batched_r_t = jnp.stack([r_t, r_t])
batched_s_t = jnp.stack([s_t, s_t])

perex_grads(theta, batched_s_tm1, batched_r_t, batched_s_t)

Array([[ 1.2,  2.4, -1.2],
       [ 1.2,  2.4, -1.2]], dtype=float32)

让我们逐个变换地进行。

首先，您将 jax.grad() 应用于 td_loss 以获得一个函数，该函数计算单个（未批处理）输入上损失相对于参数的梯度

dtdloss_dtheta = jax.grad(td_loss)

dtdloss_dtheta(theta, s_tm1, r_t, s_t)

Array([ 1.2,  2.4, -1.2], dtype=float32)

此函数计算上面数组的一行。

然后，您使用 jax.vmap() 对该函数进行矢量化。这将为所有输入和输出添加一个批处理维度。现在，给定一批输入，您将产生一批输出 - 批次中的每个输出对应于输入批次中对应成员的梯度。

almost_perex_grads = jax.vmap(dtdloss_dtheta)

batched_theta = jnp.stack([theta, theta])
almost_perex_grads(batched_theta, batched_s_tm1, batched_r_t, batched_s_t)

Array([[ 1.2,  2.4, -1.2],
       [ 1.2,  2.4, -1.2]], dtype=float32)

这并不完全是我们想要的，因为我们必须手动向该函数提供一批 theta，而实际上我们希望使用单个 theta。我们通过在 jax.vmap() 中添加 in_axes 来解决这个问题，将 theta 指定为 None，将其他参数指定为 0。这使生成的函数仅在其他参数上添加额外的轴，使 theta 保持未批处理，正如我们所希望的那样

inefficient_perex_grads = jax.vmap(dtdloss_dtheta, in_axes=(None, 0, 0, 0))

inefficient_perex_grads(theta, batched_s_tm1, batched_r_t, batched_s_t)

Array([[ 1.2,  2.4, -1.2],
       [ 1.2,  2.4, -1.2]], dtype=float32)

这实现了我们想要的功能，但速度比它应该的要慢。现在，您将整个内容包装在 jax.jit() 中，以获得相同函数的编译后的高效版本

perex_grads = jax.jit(inefficient_perex_grads)

perex_grads(theta, batched_s_tm1, batched_r_t, batched_s_t)

Array([[ 1.2,  2.4, -1.2],
       [ 1.2,  2.4, -1.2]], dtype=float32)

%timeit inefficient_perex_grads(theta, batched_s_tm1, batched_r_t, batched_s_t).block_until_ready()
%timeit perex_grads(theta, batched_s_tm1, batched_r_t, batched_s_t).block_until_ready()

10.7 ms ± 804 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)
20 μs ± 1.32 μs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)

使用 jax.grad-of-jax.grad 的 Hessian-向量积

使用高阶 jax.vmap() 可以做的一件事是构建一个 Hessian-向量积函数。（稍后您将编写一个更高效的实现，它混合了前向和逆向模式，但这个将使用纯逆向模式。）

Hessian-vector 乘积函数在 截断牛顿共轭梯度算法 中非常有用，该算法用于最小化光滑凸函数，或用于研究神经网络训练目标的曲率（例如，1，2，3，4）。

对于一个标量函数 \(f : \mathbb{R}^n \to \mathbb{R}\)，它具有连续的二阶导数（因此Hessian矩阵是对称的），在点 \(x \in \mathbb{R}^n\) 处的Hessian写成 \(\partial^2 f(x)\)。Hessian-vector 乘积函数就可以计算

\(\qquad v \mapsto \partial^2 f(x) \cdot v\)

对于任何 \(v \in \mathbb{R}^n\)。

诀窍是不实例化完整的Hessian矩阵：如果 \(n\) 很大，可能在神经网络中达到数百万甚至数十亿，那么存储Hessian矩阵可能是不可能的。

幸运的是，jax.vmap() 已经为我们提供了一种编写高效的Hessian-vector 乘积函数的方法。您只需要使用这个恒等式

\(\qquad \partial^2 f (x) v = \partial [x \mapsto \partial f(x) \cdot v] = \partial g(x)\),

其中 \(g(x) = \partial f(x) \cdot v\) 是一个新的标量函数，它将 \(f\) 在 \(x\) 处的梯度与向量 \(v\) 进行点乘。注意，您只对向量值参数的标量函数进行微分，这正是您知道 jax.vmap() 效率高的场景。

在JAX代码中，您可以这样写

def hvp(f, x, v):
    return grad(lambda x: jnp.vdot(grad(f)(x), v))(x)

这个例子表明您可以自由地使用词法闭包，JAX永远不会被扰乱或混淆。

您将在后面的几个单元格中检查这个实现，一旦您学习了如何计算密集的Hessian矩阵。您还将编写一个更好的版本，它同时使用前向模式和反向模式。

使用 jax.jacfwd 和 jax.jacrev 计算雅可比矩阵和Hessian矩阵

您可以使用 jax.jacfwd() 和 jax.jacrev() 函数计算完整的雅可比矩阵

from jax import jacfwd, jacrev

# Define a sigmoid function.
def sigmoid(x):
    return 0.5 * (jnp.tanh(x / 2) + 1)

# Outputs probability of a label being true.
def predict(W, b, inputs):
    return sigmoid(jnp.dot(inputs, W) + b)

# Build a toy dataset.
inputs = jnp.array([[0.52, 1.12,  0.77],
                   [0.88, -1.08, 0.15],
                   [0.52, 0.06, -1.30],
                   [0.74, -2.49, 1.39]])

# Initialize random model coefficients
key, W_key, b_key = random.split(key, 3)
W = random.normal(W_key, (3,))
b = random.normal(b_key, ())

# Isolate the function from the weight matrix to the predictions
f = lambda W: predict(W, b, inputs)

J = jacfwd(f)(W)
print("jacfwd result, with shape", J.shape)
print(J)

J = jacrev(f)(W)
print("jacrev result, with shape", J.shape)
print(J)

jacfwd result, with shape (4, 3)
[[ 0.05981758  0.12883787  0.08857603]
 [ 0.04015916 -0.04928625  0.00684531]
 [ 0.12188288  0.01406341 -0.3047072 ]
 [ 0.00140431 -0.00472531  0.00263782]]
jacrev result, with shape (4, 3)
[[ 0.05981757  0.12883787  0.08857603]
 [ 0.04015916 -0.04928625  0.00684531]
 [ 0.12188289  0.01406341 -0.3047072 ]
 [ 0.00140431 -0.00472531  0.00263782]]

这两个函数计算相同的值（直到机器数值），但它们的实现不同：jax.jacfwd() 使用前向模式自动微分，这对于“高”雅可比矩阵（输出比输入多）更有效，而 jax.jacrev() 使用反向模式，这对于“宽”雅可比矩阵（输入比输出多）更有效。对于接近正方形的矩阵，jax.jacfwd() 可能比 jax.jacrev() 更有效。

您也可以将 jax.jacfwd() 和 jax.jacrev() 与容器类型一起使用

def predict_dict(params, inputs):
    return predict(params['W'], params['b'], inputs)

J_dict = jacrev(predict_dict)({'W': W, 'b': b}, inputs)
for k, v in J_dict.items():
    print("Jacobian from {} to logits is".format(k))
    print(v)

Jacobian from W to logits is
[[ 0.05981757  0.12883787  0.08857603]
 [ 0.04015916 -0.04928625  0.00684531]
 [ 0.12188289  0.01406341 -0.3047072 ]
 [ 0.00140431 -0.00472531  0.00263782]]
Jacobian from b to logits is
[0.11503381 0.04563541 0.23439017 0.00189771]

有关前向模式和反向模式的更多详细信息，以及如何尽可能高效地实现 jax.jacfwd() 和 jax.jacrev()，请继续阅读！

使用这两个函数的组合，我们可以计算密集的Hessian矩阵

def hessian(f):
    return jacfwd(jacrev(f))

H = hessian(f)(W)
print("hessian, with shape", H.shape)
print(H)

hessian, with shape (4, 3, 3)
[[[ 0.02285465  0.04922541  0.03384247]
  [ 0.04922541  0.10602397  0.07289147]
  [ 0.03384247  0.07289147  0.05011288]]

 [[-0.03195215  0.03921401 -0.00544639]
  [ 0.03921401 -0.04812629  0.00668421]
  [-0.00544639  0.00668421 -0.00092836]]

 [[-0.01583708 -0.00182736  0.03959271]
  [-0.00182736 -0.00021085  0.00456839]
  [ 0.03959271  0.00456839 -0.09898177]]

 [[-0.00103524  0.00348343 -0.00194457]
  [ 0.00348343 -0.01172127  0.0065432 ]
  [-0.00194457  0.0065432  -0.00365263]]]

这个形状是有意义的：如果您从一个函数 \(f : \mathbb{R}^n \to \mathbb{R}^m\) 开始，那么在一个点 \(x \in \mathbb{R}^n\) 处，您期望得到以下形状

• \(f(x) \in \mathbb{R}^m\)，\(f\) 在 \(x\) 处的函数值，

• \(\partial f(x) \in \mathbb{R}^{m \times n}\)，在 \(x\) 处的雅可比矩阵，

• \(\partial^2 f(x) \in \mathbb{R}^{m \times n \times n}\)，在 \(x\) 处的Hessian，

等等。

要实现 hessian，您可以使用 jacfwd(jacrev(f)) 或 jacrev(jacfwd(f)) 或这两个函数的任何其他组合。但前向-反向组合通常是最有效的。这是因为在内部雅可比计算中，我们通常对一个宽雅可比函数进行微分（可能像损失函数 \(f : \mathbb{R}^n \to \mathbb{R}\)），而在外部雅可比计算中，我们对一个具有方形雅可比的函数进行微分（因为 \(\nabla f : \mathbb{R}^n \to \mathbb{R}^n\)），这就是前向模式胜出的地方。

它是如何实现的：两个基础的自动微分函数

雅可比-向量乘积（JVP，也称为前向模式自动微分）

JAX 包含高效且通用的前向模式和反向模式自动微分实现。我们熟悉的 jax.vmap() 函数是基于反向模式构建的，但为了解释两种模式之间的区别以及何时使用哪种模式，您需要一些数学背景。

JVP 在数学中的应用

在数学上，给定一个函数 \(f : \mathbb{R}^n \to \mathbb{R}^m\)，\(f\) 在一个输入点 \(x \in \mathbb{R}^n\) 处的雅可比矩阵，记为 \(\partial f(x)\)，通常被认为是 \(\mathbb{R}^m \times \mathbb{R}^n\) 中的一个矩阵

\(\qquad \partial f(x) \in \mathbb{R}^{m \times n}\).

但您也可以将 \(\partial f(x)\) 视为一个线性映射，它将 \(f\) 在点 \(x\) 处的域的切空间（这只是 \(\mathbb{R}^n\) 的另一个副本）映射到 \(f\) 在点 \(f(x)\) 处的陪域的切空间（\(\mathbb{R}^m\) 的副本）

\(\qquad \partial f(x) : \mathbb{R}^n \to \mathbb{R}^m\).

这个映射被称为 \(f\) 在 \(x\) 处的 前推映射。雅可比矩阵只是这个线性映射在标准基上的矩阵。

如果您不确定一个具体的输入点 \(x\)，那么您可以将函数 \(\partial f\) 视为首先接收一个输入点，然后返回该输入点处的雅可比线性映射

\(\qquad \partial f : \mathbb{R}^n \to \mathbb{R}^n \to \mathbb{R}^m\).

特别是，您可以取消柯里化，这样给定输入点 \(x \in \mathbb{R}^n\) 和一个切向量 \(v \in \mathbb{R}^n\)，您会得到一个输出切向量，位于 \(\mathbb{R}^m\) 中。我们将从 \((x, v)\) 对到输出切向量的映射称为 *雅可比-向量乘积*，并将其写为

\(\qquad (x, v) \mapsto \partial f(x) v\)

JVP 在 JAX 代码中的应用

回到 Python 代码，JAX 的 jax.jvp() 函数模拟了这种转换。给定一个评估 \(f\) 的 Python 函数，JAX 的 jax.jvp() 函数提供了一种方法来获取一个 Python 函数，用于评估 \((x, v) \mapsto (f(x), \partial f(x) v)\)。

from jax import jvp

# Isolate the function from the weight matrix to the predictions
f = lambda W: predict(W, b, inputs)

key, subkey = random.split(key)
v = random.normal(subkey, W.shape)

# Push forward the vector `v` along `f` evaluated at `W`
y, u = jvp(f, (W,), (v,))

从 类似 Haskell 的类型签名 的角度来看，您可以这样写

jvp :: (a -> b) -> a -> T a -> (b, T b)

其中 T a 用于表示 a 的切空间的类型。

换句话说，jvp 函数接受三个参数：一个类型为 a -> b 的函数，一个类型为 a 的值，以及一个类型为 T a 的切向量值。它返回一个包含类型为 b 的值和类型为 T b 的输出切向量的对。

对 jvp 函数进行转换后的函数的评估方式与原始函数类似，但它将类型为 a 的每个原始值与类型为 T a 的切向量值配对。对于原始函数要应用的每个基本数值运算，jvp 函数转换后的函数会执行该基本运算的“JVP 规则”，该规则既会在原始值上评估基本运算，也会在这些原始值上应用基本运算的 JVP。

这种评估策略对计算复杂度有一些直接的影响。由于我们在进行时评估 JVP，因此我们不需要存储任何东西以备后用，因此内存成本与计算深度无关。此外，jvp 变换函数的 FLOP 成本约为评估函数成本的 3 倍（评估原始函数的成本为一个工作单位，例如 sin(x)；线性化的成本为一个工作单位，例如 cos(x)；将线性化函数应用于向量的成本为一个工作单位，例如 cos_x * v）。换句话说，对于固定的原始点 \(x\)，我们可以评估 \(v \mapsto \partial f(x) \cdot v\)，其边际成本与评估 \(f\) 的成本大致相同。

这种内存复杂度听起来非常有说服力！那么为什么我们在机器学习中很少看到正向模式呢？

为了回答这个问题，首先考虑如何使用 JVP 构建完整的雅可比矩阵。如果我们将 JVP 应用于单热切线向量，它将揭示雅可比矩阵的一列，对应于我们输入的非零项。因此我们可以一次构建一列完整的雅可比矩阵，并且获取每列的成本大约相当于一次函数评估。这对具有“高”雅可比矩阵的函数将是有效的，但对于具有“宽”雅可比矩阵的函数则效率低下。

如果您在机器学习中进行基于梯度的优化，您可能希望最小化从 \(\mathbb{R}^n\) 中的参数到 \(\mathbb{R}\) 中的标量损失值的损失函数。这意味着此函数的雅可比矩阵是一个非常宽的矩阵：\(\partial f(x) \in \mathbb{R}^{1 \times n}\)，我们通常将其与梯度向量 \(\nabla f(x) \in \mathbb{R}^n\) 等同起来。一次构建一列矩阵，每次调用消耗的 FLOP 数量与评估原始函数的 FLOP 数量类似，这似乎效率低下！特别是对于训练神经网络，其中 \(f\) 是训练损失函数，而 \(n\) 可能达到数百万甚至数十亿，这种方法根本无法扩展。

为了更好地处理此类函数，您只需要使用反向模式。

向量-雅可比积 (VJP，也称为反向模式自动微分)

正向模式为我们提供了一个评估雅可比-向量积的函数，我们可以使用它一次构建一列雅可比矩阵，而反向模式是一种获取评估向量-雅可比积（等效于雅可比转置-向量积）的函数的方法，我们可以使用它一次构建一行的雅可比矩阵。

数学中的 VJP

让我们再次考虑一个函数 \(f : \mathbb{R}^n \to \mathbb{R}^m\)。从 JVP 的符号开始，VJP 的符号非常简单

\(\qquad (x, v) \mapsto v \partial f(x)\),

其中 \(v\) 是 \(f\) 在 \(x\) 处的余切空间的元素（与 \(\mathbb{R}^m\) 的另一个副本同构）。在严格的情况下，我们应该将 \(v\) 看作一个线性映射 \(v : \mathbb{R}^m \to \mathbb{R}\)，当我们写 \(v \partial f(x)\) 时，我们的意思是函数复合 \(v \circ \partial f(x)\)，其中类型是由于 \(\partial f(x) : \mathbb{R}^n \to \mathbb{R}^m\) 而得出的。但在常见情况下，我们可以将 \(v\) 与 \(\mathbb{R}^m\) 中的一个向量等同起来，并且几乎可以互换使用，就像我们有时可能在“列向量”和“行向量”之间来回切换而没有太多评论一样。

有了这种等同关系，我们可以将 VJP 的线性部分看作是 JVP 的线性部分的转置（或伴随共轭）

\(\qquad (x, v) \mapsto \partial f(x)^\mathsf{T} v\).

对于给定的点 \(x\)，我们可以将签名写为

\(\qquad \partial f(x)^\mathsf{T} : \mathbb{R}^m \to \mathbb{R}^n\).

在余切空间上的相应映射通常被称为 \(f\) 在 \(x\) 处的 拉回。对于我们的目的来说，关键是它从看起来像 \(f\) 输出的东西到看起来像 \(f\) 输入的东西，就像我们可能从转置的线性函数中期望的那样。

JAX 代码中的 VJP

从数学回到 Python，JAX 函数 vjp 可以接收一个用于评估 \(f\) 的 Python 函数，并为我们返回一个用于评估 VJP \((x, v) \mapsto (f(x), v^\mathsf{T} \partial f(x))\) 的 Python 函数。

from jax import vjp

# Isolate the function from the weight matrix to the predictions
f = lambda W: predict(W, b, inputs)

y, vjp_fun = vjp(f, W)

key, subkey = random.split(key)
u = random.normal(subkey, y.shape)

# Pull back the covector `u` along `f` evaluated at `W`
v = vjp_fun(u)

在 类似 Haskell 的类型签名 方面，我们可以写为

vjp :: (a -> b) -> a -> (b, CT b -> CT a)

其中我们使用 CT a 来表示 a 的余切空间的类型。换句话说，vjp 接收类型为 a -> b 的函数和类型为 a 的点作为参数，并返回一个包含类型为 b 的值和类型为 CT b -> CT a 的线性映射的元组。

这很棒，因为它允许我们一次构建一行的雅可比矩阵，并且评估 \((x, v) \mapsto (f(x), v^\mathsf{T} \partial f(x))\) 的 FLOP 成本仅为评估 \(f\) 的成本的三倍左右。特别是，如果我们想要函数 \(f : \mathbb{R}^n \to \mathbb{R}\) 的梯度，我们可以通过一次调用来完成。这就是 jax.vmap() 对基于梯度的优化有效的原因，即使是对数百万甚至数十亿参数的神经网络训练损失函数等目标也是如此。

但是，也有一些成本：虽然 FLOP 友好，但内存会随着计算深度的增加而扩展。此外，实现传统上比正向模式更复杂，尽管 JAX 有一些秘密武器（这是以后笔记本电脑的主题！）。

要了解更多关于反向模式的工作原理，请查看 2017 年深度学习暑期学校的这个教程视频。

使用 VJP 的向量值梯度

如果您有兴趣获取向量值梯度（例如 tf.gradients）

def vgrad(f, x):
  y, vjp_fn = vjp(f, x)
  return vjp_fn(jnp.ones(y.shape))[0]

print(vgrad(lambda x: 3*x**2, jnp.ones((2, 2))))

[[6. 6.]
 [6. 6.]]

使用正向模式和反向模式的 Hessian-向量积

在上一节中，您使用反向模式实现了一个 Hessian-向量积函数（假设连续二阶导数）

def hvp(f, x, v):
    return grad(lambda x: jnp.vdot(grad(f)(x), v))(x)

这很有效，但您可以做得更好，并通过使用正向模式和反向模式来节省一些内存。

在数学上，给定一个要微分的函数 \(f : \mathbb{R}^n \to \mathbb{R}\)、一个线性化函数的点 \(x \in \mathbb{R}^n\) 和一个向量 \(v \in \mathbb{R}^n\)，我们想要的 Hessian-向量积函数是

\((x, v) \mapsto \partial^2 f(x) v\)

考虑辅助函数 \(g : \mathbb{R}^n \to \mathbb{R}^n\)，其定义为 \(f\) 的导数（或梯度），即 \(g(x) = \partial f(x)\)。您只需要它的 JVP，因为它将为我们提供

\((x, v) \mapsto \partial g(x) v = \partial^2 f(x) v\).

我们可以将它几乎直接转换为代码

# forward-over-reverse
def hvp(f, primals, tangents):
  return jvp(grad(f), primals, tangents)[1]

更好的是，由于您不需要直接调用 jnp.dot()，因此此 hvp 函数适用于任何形状的数组，以及任意容器类型（例如作为嵌套列表/字典/元组存储的向量），甚至不依赖于 jax.numpy。

以下是如何使用它的示例

def f(X):
  return jnp.sum(jnp.tanh(X)**2)

key, subkey1, subkey2 = random.split(key, 3)
X = random.normal(subkey1, (30, 40))
V = random.normal(subkey2, (30, 40))

ans1 = hvp(f, (X,), (V,))
ans2 = jnp.tensordot(hessian(f)(X), V, 2)

print(jnp.allclose(ans1, ans2, 1e-4, 1e-4))

True

您可能考虑的另一种编写方法是使用反向-正向

# Reverse-over-forward
def hvp_revfwd(f, primals, tangents):
  g = lambda primals: jvp(f, primals, tangents)[1]
  return grad(g)(primals)

但这并不太好，因为正向模式的开销小于反向模式，并且由于此处的外部微分运算符必须比内部微分运算符微分更大的计算，因此在外层保留正向模式效果最佳

# Reverse-over-reverse, only works for single arguments
def hvp_revrev(f, primals, tangents):
  x, = primals
  v, = tangents
  return grad(lambda x: jnp.vdot(grad(f)(x), v))(x)


print("Forward over reverse")
%timeit -n10 -r3 hvp(f, (X,), (V,))
print("Reverse over forward")
%timeit -n10 -r3 hvp_revfwd(f, (X,), (V,))
print("Reverse over reverse")
%timeit -n10 -r3 hvp_revrev(f, (X,), (V,))

print("Naive full Hessian materialization")
%timeit -n10 -r3 jnp.tensordot(hessian(f)(X), V, 2)

Forward over reverse
10.3 ms ± 773 μs per loop (mean ± std. dev. of 3 runs, 10 loops each)
Reverse over forward
The slowest run took 4.60 times longer than the fastest. This could mean that an intermediate result is being cached.
23.6 ms ± 18.1 ms per loop (mean ± std. dev. of 3 runs, 10 loops each)
Reverse over reverse
The slowest run took 4.31 times longer than the fastest. This could mean that an intermediate result is being cached.
32.7 ms ± 24.3 ms per loop (mean ± std. dev. of 3 runs, 10 loops each)
Naive full Hessian materialization
86.3 ms ± 7.57 ms per loop (mean ± std. dev. of 3 runs, 10 loops each)

组合 VJP、JVP 和 jax.vmap

雅可比矩阵和矩阵-雅可比积

现在您有了 jax.jvp() 和 jax.vjp() 变换，它们可以为您提供一次向前推进或向后拉回单个向量的函数，您可以使用 JAX 的 jax.vmap() 变换 来一次性向前推进或向后拉回整个基。特别是，您可以使用它来编写快速矩阵-雅可比积和雅可比矩阵-积

# Isolate the function from the weight matrix to the predictions
f = lambda W: predict(W, b, inputs)

# Pull back the covectors `m_i` along `f`, evaluated at `W`, for all `i`.
# First, use a list comprehension to loop over rows in the matrix M.
def loop_mjp(f, x, M):
    y, vjp_fun = vjp(f, x)
    return jnp.vstack([vjp_fun(mi) for mi in M])

# Now, use vmap to build a computation that does a single fast matrix-matrix
# multiply, rather than an outer loop over vector-matrix multiplies.
def vmap_mjp(f, x, M):
    y, vjp_fun = vjp(f, x)
    outs, = vmap(vjp_fun)(M)
    return outs

key = random.key(0)
num_covecs = 128
U = random.normal(key, (num_covecs,) + y.shape)

loop_vs = loop_mjp(f, W, M=U)
print('Non-vmapped Matrix-Jacobian product')
%timeit -n10 -r3 loop_mjp(f, W, M=U)

print('\nVmapped Matrix-Jacobian product')
vmap_vs = vmap_mjp(f, W, M=U)
%timeit -n10 -r3 vmap_mjp(f, W, M=U)

assert jnp.allclose(loop_vs, vmap_vs), 'Vmap and non-vmapped Matrix-Jacobian Products should be identical'

Non-vmapped Matrix-Jacobian product
388 ms ± 3.44 ms per loop (mean ± std. dev. of 3 runs, 10 loops each)

Vmapped Matrix-Jacobian product
10.6 ms ± 261 μs per loop (mean ± std. dev. of 3 runs, 10 loops each)

/tmp/ipykernel_647/3769736790.py:8: DeprecationWarning: vstack requires ndarray or scalar arguments, got <class 'tuple'> at position 0. In a future JAX release this will be an error.
  return jnp.vstack([vjp_fun(mi) for mi in M])

def loop_jmp(f, W, M):
    # jvp immediately returns the primal and tangent values as a tuple,
    # so we'll compute and select the tangents in a list comprehension
    return jnp.vstack([jvp(f, (W,), (mi,))[1] for mi in M])

def vmap_jmp(f, W, M):
    _jvp = lambda s: jvp(f, (W,), (s,))[1]
    return vmap(_jvp)(M)

num_vecs = 128
S = random.normal(key, (num_vecs,) + W.shape)

loop_vs = loop_jmp(f, W, M=S)
print('Non-vmapped Jacobian-Matrix product')
%timeit -n10 -r3 loop_jmp(f, W, M=S)
vmap_vs = vmap_jmp(f, W, M=S)
print('\nVmapped Jacobian-Matrix product')
%timeit -n10 -r3 vmap_jmp(f, W, M=S)

assert jnp.allclose(loop_vs, vmap_vs), 'Vmap and non-vmapped Jacobian-Matrix products should be identical'

Non-vmapped Jacobian-Matrix product
394 ms ± 8.24 ms per loop (mean ± std. dev. of 3 runs, 10 loops each)

Vmapped Jacobian-Matrix product
4.88 ms ± 192 μs per loop (mean ± std. dev. of 3 runs, 10 loops each)

jax.jacfwd 和 jax.jacrev 的实现

现在我们已经看到了快速的雅可比矩阵-积和矩阵-雅可比积，不难猜测如何编写 jax.jacfwd() 和 jax.jacrev()。我们只需要使用相同的方法一次性向前推进或向后拉回整个标准基（与单位矩阵同构）。

from jax import jacrev as builtin_jacrev

def our_jacrev(f):
    def jacfun(x):
        y, vjp_fun = vjp(f, x)
        # Use vmap to do a matrix-Jacobian product.
        # Here, the matrix is the Euclidean basis, so we get all
        # entries in the Jacobian at once.
        J, = vmap(vjp_fun, in_axes=0)(jnp.eye(len(y)))
        return J
    return jacfun

assert jnp.allclose(builtin_jacrev(f)(W), our_jacrev(f)(W)), 'Incorrect reverse-mode Jacobian results!'

from jax import jacfwd as builtin_jacfwd

def our_jacfwd(f):
    def jacfun(x):
        _jvp = lambda s: jvp(f, (x,), (s,))[1]
        Jt = vmap(_jvp, in_axes=1)(jnp.eye(len(x)))
        return jnp.transpose(Jt)
    return jacfun

assert jnp.allclose(builtin_jacfwd(f)(W), our_jacfwd(f)(W)), 'Incorrect forward-mode Jacobian results!'

有趣的是，Autograd 库无法做到这一点。Autograd 中反向模式 jacobian 的 实现 必须使用外层循环 map 一次拉回一个向量。一次将一个向量推入计算比使用 jax.vmap() 将所有向量一起批处理效率低得多。

Autograd 无法做的另一件事是 jax.jit()。有趣的是，无论在待求导函数中使用多少 Python 动态性，我们始终可以在计算的线性部分使用 jax.jit()。例如

def f(x):
    try:
        if x < 3:
            return 2 * x ** 3
        else:
            raise ValueError
    except ValueError:
        return jnp.pi * x

y, f_vjp = vjp(f, 4.)
print(jit(f_vjp)(1.))

(Array(3.1415927, dtype=float32, weak_type=True),)

复数和微分

JAX 在复数和微分方面表现出色。为了支持 全纯和非全纯微分，最好从 JVP 和 VJP 的角度思考。

考虑一个复数到复数的函数 \(f: \mathbb{C} \to \mathbb{C}\)，并将其与相应的函数 \(g: \mathbb{R}^2 \to \mathbb{R}^2\) 相对应。

def f(z):
  x, y = jnp.real(z), jnp.imag(z)
  return u(x, y) + v(x, y) * 1j

def g(x, y):
  return (u(x, y), v(x, y))

也就是说，我们已经分解了 \(f(z) = u(x, y) + v(x, y) i\)，其中 \(z = x + y i\)，并将 \(\mathbb{C}\) 与 \(\mathbb{R}^2\) 对应起来得到 \(g\)。

由于 \(g\) 只涉及实数输入和输出，因此我们已经知道如何为其编写雅可比向量积，例如给定一个切向量 \((c, d) \in \mathbb{R}^2\)，即

\(\begin{bmatrix} \partial_0 u(x, y) & \partial_1 u(x, y) \\ \partial_0 v(x, y) & \partial_1 v(x, y) \end{bmatrix} \begin{bmatrix} c \\ d \end{bmatrix}\).

为了得到原始函数 \(f\) 应用于切向量 \(c + di \in \mathbb{C}\) 的 JVP，我们只需使用相同的定义并将结果识别为另一个复数，

\(\partial f(x + y i)(c + d i) = \begin{matrix} \begin{bmatrix} 1 & i \end{bmatrix} \\ ~ \end{matrix} \begin{bmatrix} \partial_0 u(x, y) & \partial_1 u(x, y) \\ \partial_0 v(x, y) & \partial_1 v(x, y) \end{bmatrix} \begin{bmatrix} c \\ d \end{bmatrix}\).

这就是我们对 \(\mathbb{C} \to \mathbb{C}\) 函数的 JVP 的定义！请注意，\(f\) 是否为全纯并不重要：JVP 是明确的。

这里有一个检查

def check(seed):
  key = random.key(seed)

  # random coeffs for u and v
  key, subkey = random.split(key)
  a, b, c, d = random.uniform(subkey, (4,))

  def fun(z):
    x, y = jnp.real(z), jnp.imag(z)
    return u(x, y) + v(x, y) * 1j

  def u(x, y):
    return a * x + b * y

  def v(x, y):
    return c * x + d * y

  # primal point
  key, subkey = random.split(key)
  x, y = random.uniform(subkey, (2,))
  z = x + y * 1j

  # tangent vector
  key, subkey = random.split(key)
  c, d = random.uniform(subkey, (2,))
  z_dot = c + d * 1j

  # check jvp
  _, ans = jvp(fun, (z,), (z_dot,))
  expected = (grad(u, 0)(x, y) * c +
              grad(u, 1)(x, y) * d +
              grad(v, 0)(x, y) * c * 1j+
              grad(v, 1)(x, y) * d * 1j)
  print(jnp.allclose(ans, expected))

check(0)
check(1)
check(2)

True
True
True

VJP 怎么样？我们做一些非常相似的事情：对于一个余切向量 \(c + di \in \mathbb{C}\)，我们将 \(f\) 的 VJP 定义为

\((c + di)^* \; \partial f(x + y i) = \begin{matrix} \begin{bmatrix} c & -d \end{bmatrix} \\ ~ \end{matrix} \begin{bmatrix} \partial_0 u(x, y) & \partial_1 u(x, y) \\ \partial_0 v(x, y) & \partial_1 v(x, y) \end{bmatrix} \begin{bmatrix} 1 \\ -i \end{bmatrix}\).

为什么会有负号？它们只是为了处理复数共轭以及我们正在处理余向量这一事实。

这里是对 VJP 规则的检查

def check(seed):
  key = random.key(seed)

  # random coeffs for u and v
  key, subkey = random.split(key)
  a, b, c, d = random.uniform(subkey, (4,))

  def fun(z):
    x, y = jnp.real(z), jnp.imag(z)
    return u(x, y) + v(x, y) * 1j

  def u(x, y):
    return a * x + b * y

  def v(x, y):
    return c * x + d * y

  # primal point
  key, subkey = random.split(key)
  x, y = random.uniform(subkey, (2,))
  z = x + y * 1j

  # cotangent vector
  key, subkey = random.split(key)
  c, d = random.uniform(subkey, (2,))
  z_bar = jnp.array(c + d * 1j)  # for dtype control

  # check vjp
  _, fun_vjp = vjp(fun, z)
  ans, = fun_vjp(z_bar)
  expected = (grad(u, 0)(x, y) * c +
              grad(v, 0)(x, y) * (-d) +
              grad(u, 1)(x, y) * c * (-1j) +
              grad(v, 1)(x, y) * (-d) * (-1j))
  assert jnp.allclose(ans, expected, atol=1e-5, rtol=1e-5)

check(0)
check(1)
check(2)

像 jax.grad()、jax.jacfwd() 和 jax.jacrev() 这样的便捷包装器怎么样？

对于 \(\mathbb{R} \to \mathbb{R}\) 函数，回想一下我们定义了 grad(f)(x) 为 vjp(f, x)[1](1.0)，这是可行的，因为将 VJP 应用于一个 1.0 值会揭示梯度（即雅可比矩阵或导数）。我们可以对 \(\mathbb{C} \to \mathbb{R}\) 函数做同样的事情：我们仍然可以使用 1.0 作为余切向量，我们只会得到一个总结完整雅可比矩阵的复数结果

def f(z):
  x, y = jnp.real(z), jnp.imag(z)
  return x**2 + y**2

z = 3. + 4j
grad(f)(z)

Array(6.-8.j, dtype=complex64)

对于一般 \(\mathbb{C} \to \mathbb{C}\) 函数，雅可比矩阵有 4 个实值自由度（如上面的 2x2 雅可比矩阵），因此我们不能希望用一个复数来表示它们。但对于全纯函数，我们可以做到！全纯函数恰好是一个 \(\mathbb{C} \to \mathbb{C}\) 函数，具有其导数可以用单个复数表示的特殊性质。（柯西-黎曼方程 确保上面的 2x2 雅可比矩阵具有复平面上缩放和旋转矩阵的特殊形式，即单个复数在乘法下的作用。）我们可以使用单个调用来揭示这个复数。 vjp，余向量为 1.0。

由于这只有效于全纯函数，因此要使用此技巧，我们需要向 JAX 保证我们的函数是全纯的；否则，当使用 jax.grad() 针对复数输出函数时，JAX 会引发错误

def f(z):
  return jnp.sin(z)

z = 3. + 4j
grad(f, holomorphic=True)(z)

Array(-27.034946-3.8511534j, dtype=complex64, weak_type=True)

所有 holomorphic=True 保证做的只是在输出为复数值时禁用错误。当函数不是全纯时，我们仍然可以编写 holomorphic=True，但我们得到的答案将不会表示完整的雅可比矩阵。相反，它将是函数的雅可比矩阵，其中我们只是丢弃了输出的虚部

def f(z):
  return jnp.conjugate(z)

z = 3. + 4j
grad(f, holomorphic=True)(z)  # f is not actually holomorphic!

Array(1.-0.j, dtype=complex64, weak_type=True)

这里有一些关于 jax.grad() 在这里工作方式的有用结果

1. 我们可以对全纯 \(\mathbb{C} \to \mathbb{C}\) 函数使用 jax.grad()。

2. 我们可以使用 jax.grad() 来优化 \(f : \mathbb{C} \to \mathbb{R}\) 函数，例如复参数 x 的实值损失函数，方法是沿 grad(f)(x) 共轭的方向迈进。

3. 如果我们有一个 \(\mathbb{R} \to \mathbb{R}\) 函数，它恰好使用了一些内部的复数运算（其中一些必须是非全纯的，例如卷积中使用的 FFT），那么 jax.grad() 仍然有效，我们得到的结果与仅使用实数值的实现得到的结果相同。

无论如何，JVP 和 VJP 始终是明确的。如果我们想要计算非全纯 \(\mathbb{C} \to \mathbb{C}\) 函数的完整雅可比矩阵，我们可以使用 JVP 或 VJP 来做到这一点！

您应该期望复数在 JAX 中的任何地方都能正常工作。以下是微分通过复矩阵的 Cholesky 分解的示例

A = jnp.array([[5.,    2.+3j,    5j],
              [2.-3j,   7.,  1.+7j],
              [-5j,  1.-7j,    12.]])

def f(X):
    L = jnp.linalg.cholesky(X)
    return jnp.sum((L - jnp.sin(L))**2)

grad(f, holomorphic=True)(A)

Array([[-0.7534186  +0.j       , -3.0509028 -10.940544j ,
         5.9896846  +3.5423026j],
       [-3.0509028 +10.940544j , -8.904491   +0.j       ,
        -5.1351523  -6.559373j ],
       [ 5.9896846  -3.5423026j, -5.1351523  +6.559373j ,
         0.01320427 +0.j       ]], dtype=complex64)

JAX 可转换 Python 函数的自定义导数规则

JAX 中有两种定义微分规则的方法

1. 使用 jax.custom_jvp() 和 jax.custom_vjp() 为已经是 JAX 可转换的 Python 函数定义自定义微分规则；以及

2. 定义新的 core.Primitive 实例以及所有它们的转换规则，例如调用来自其他系统（如求解器、模拟器或通用数值计算系统）的函数。

这个笔记本是关于 #1 的。要阅读关于 #2 的信息，请参阅 关于添加原语的笔记本。

TL;DR：使用 jax.custom_jvp() 的自定义 JVP

from jax import custom_jvp

@custom_jvp
def f(x, y):
  return jnp.sin(x) * y

@f.defjvp
def f_jvp(primals, tangents):
  x, y = primals
  x_dot, y_dot = tangents
  primal_out = f(x, y)
  tangent_out = jnp.cos(x) * x_dot * y + jnp.sin(x) * y_dot
  return primal_out, tangent_out

print(f(2., 3.))
y, y_dot = jvp(f, (2., 3.), (1., 0.))
print(y)
print(y_dot)
print(grad(f)(2., 3.))

2.7278922
2.7278922
-1.2484405
-1.2484405

# Equivalent alternative using the `defjvps` convenience wrapper

@custom_jvp
def f(x, y):
  return jnp.sin(x) * y

f.defjvps(lambda x_dot, primal_out, x, y: jnp.cos(x) * x_dot * y,
          lambda y_dot, primal_out, x, y: jnp.sin(x) * y_dot)

print(f(2., 3.))
y, y_dot = jvp(f, (2., 3.), (1., 0.))
print(y)
print(y_dot)
print(grad(f)(2., 3.))

2.7278922
2.7278922
-1.2484405
-1.2484405

TL;DR：使用 jax.custom_vjp 的自定义 VJP

from jax import custom_vjp

@custom_vjp
def f(x, y):
  return jnp.sin(x) * y

def f_fwd(x, y):
# Returns primal output and residuals to be used in backward pass by `f_bwd`.
  return f(x, y), (jnp.cos(x), jnp.sin(x), y)

def f_bwd(res, g):
  cos_x, sin_x, y = res # Gets residuals computed in `f_fwd`
  return (cos_x * g * y, sin_x * g)

f.defvjp(f_fwd, f_bwd)

print(grad(f)(2., 3.))

-1.2484405

示例问题

为了了解 jax.custom_jvp() 和 jax.custom_vjp() 的作用，让我们看一下几个例子。下一节将详细介绍 jax.custom_jvp() 和 jax.custom_vjp() API。

示例：数值稳定性

jax.custom_jvp() 的一个应用是提高微分的数值稳定性。

假设我们要编写一个名为 log1pexp 的函数，该函数计算 \(x \mapsto \log ( 1 + e^x )\)。我们可以使用 jax.numpy 来编写它

def log1pexp(x):
  return jnp.log(1. + jnp.exp(x))

log1pexp(3.)

Array(3.0485873, dtype=float32, weak_type=True)

由于它是使用 jax.numpy 编写的，因此它是 JAX 可转换的

print(jit(log1pexp)(3.))
print(jit(grad(log1pexp))(3.))
print(vmap(jit(grad(log1pexp)))(jnp.arange(3.)))

3.0485873
0.95257413
[0.5       0.7310586 0.8807971]

但这里潜藏着一个数值稳定性问题

print(grad(log1pexp)(100.))

nan

这似乎不对！毕竟，\(x \mapsto \log (1 + e^x)\) 的导数是 \(x \mapsto \frac{e^x}{1 + e^x}\)，因此对于 \(x\) 的较大值，我们预计该值约为 1。

我们可以通过查看梯度计算的 jaxpr 来更深入地了解发生了什么

from jax import make_jaxpr

make_jaxpr(grad(log1pexp))(100.)

{ lambda ; a:f32[]. let
    b:f32[] = exp a
    c:f32[] = add 1.0 b
    _:f32[] = log c
    d:f32[] = div 1.0 c
    e:f32[] = mul d b
  in (e,) }

逐步跟踪 jaxpr 的评估过程，请注意，最后一行会涉及对浮点数运算会舍入为 0 和 \(\infty\) 的值的乘法，这从来不是一个好主意。也就是说，我们实际上是在评估 lambda x: (1 / (1 + jnp.exp(x))) * jnp.exp(x) 的值，其中 x 很大，这实际上变成了 0. * jnp.inf。

与其生成如此大的值和如此小的值，并期望浮点数无法始终提供的抵消，我们宁愿将导数函数表示为一个数值上更稳定的程序。特别是，我们可以编写一个更接近地评估等价数学表达式 \(1 - \frac{1}{1 + e^x}\) 的程序，而没有任何抵消现象。

这个问题很有趣，因为即使我们对 log1pexp 的定义已经可以进行 JAX 微分（并使用 jax.jit()，jax.vmap()，… 进行转换），我们对将标准自动微分规则应用于构成 log1pexp 的基本运算并组合结果的效果并不满意。相反，我们希望指定整个函数 log1pexp 应该如何作为整体进行微分，从而更好地排列这些指数。

这是对已经可以进行 JAX 转换的 Python 函数的自定义导数规则的一个应用：指定复合函数应该如何进行微分，同时仍然使用其原始 Python 定义进行其他转换（例如 jax.jit()，jax.vmap()，…）。

这是一个使用 jax.custom_jvp() 的解决方案

@custom_jvp
def log1pexp(x):
  return jnp.log(1. + jnp.exp(x))

@log1pexp.defjvp
def log1pexp_jvp(primals, tangents):
  x, = primals
  x_dot, = tangents
  ans = log1pexp(x)
  ans_dot = (1 - 1/(1 + jnp.exp(x))) * x_dot
  return ans, ans_dot

print(grad(log1pexp)(100.))

1.0

print(jit(log1pexp)(3.))
print(jit(grad(log1pexp))(3.))
print(vmap(jit(grad(log1pexp)))(jnp.arange(3.)))

3.0485873
0.95257413
[0.5       0.7310586 0.8807971]

这是一个 defjvps 辅助包装器，用于表达相同的内容

@custom_jvp
def log1pexp(x):
  return jnp.log(1. + jnp.exp(x))

log1pexp.defjvps(lambda t, ans, x: (1 - 1/(1 + jnp.exp(x))) * t)

print(grad(log1pexp)(100.))
print(jit(log1pexp)(3.))
print(jit(grad(log1pexp))(3.))
print(vmap(jit(grad(log1pexp)))(jnp.arange(3.)))

1.0
3.0485873
0.95257413
[0.5       0.7310586 0.8807971]

示例：强制执行微分约定

一个相关的应用是强制执行微分约定，可能是在边界处。

考虑函数 \(f : \mathbb{R}_+ \to \mathbb{R}_+\)，其中 \(f(x) = \frac{x}{1 + \sqrt{x}}\)，其中我们取 \(\mathbb{R}_+ = [0, \infty)\)。我们可能将 \(f\) 实现为类似这样的程序

def f(x):
  return x / (1 + jnp.sqrt(x))

作为 \(\mathbb{R}\)（整个实数轴）上的数学函数，\(f\) 在零处不可微（因为定义导数的极限从左侧不存在）。相应地，自动微分会生成一个 nan 值

print(grad(f)(0.))

nan

但在数学上，如果我们将 \(f\) 视为 \(\mathbb{R}_+\) 上的函数，那么它在 0 处是可微的 [Rudin’s Principles of Mathematical Analysis 定理 5.1，或 Tao’s Analysis I 第 3 版定理 10.1.1 和例 10.1.6]。或者，我们也可以说，按照约定，我们希望考虑从右侧的导数。因此，Python 函数 grad(f) 在 0.0 处返回的值有一个合理的意义，即 1.0。默认情况下，JAX 的微分机制假定所有函数都定义在 \(\mathbb{R}\) 上，因此在这里不会生成 1.0。

我们可以使用自定义 JVP 规则！特别是，我们可以根据 \(\mathbb{R}_+\) 上的导数函数 \(x \mapsto \frac{\sqrt{x} + 2}{2(\sqrt{x} + 1)^2}\) 来定义 JVP 规则，

@custom_jvp
def f(x):
  return x / (1 + jnp.sqrt(x))

@f.defjvp
def f_jvp(primals, tangents):
  x, = primals
  x_dot, = tangents
  ans = f(x)
  ans_dot = ((jnp.sqrt(x) + 2) / (2 * (jnp.sqrt(x) + 1)**2)) * x_dot
  return ans, ans_dot

print(grad(f)(0.))

1.0

这是辅助包装器版本

@custom_jvp
def f(x):
  return x / (1 + jnp.sqrt(x))

f.defjvps(lambda t, ans, x: ((jnp.sqrt(x) + 2) / (2 * (jnp.sqrt(x) + 1)**2)) * t)

print(grad(f)(0.))

1.0

示例：梯度裁剪

在某些情况下我们希望表达一个数学微分运算时，在其他情况下我们甚至可能希望脱离数学来调整自动微分执行的运算。一个典型的例子是反向模式梯度裁剪。

对于梯度裁剪，我们可以使用 jnp.clip() 以及一个仅适用于反向模式的 jax.custom_vjp() 规则

from functools import partial

@custom_vjp
def clip_gradient(lo, hi, x):
  return x  # identity function

def clip_gradient_fwd(lo, hi, x):
  return x, (lo, hi)  # save bounds as residuals

def clip_gradient_bwd(res, g):
  lo, hi = res
  return (None, None, jnp.clip(g, lo, hi))  # use None to indicate zero cotangents for lo and hi

clip_gradient.defvjp(clip_gradient_fwd, clip_gradient_bwd)

import matplotlib.pyplot as plt

t = jnp.linspace(0, 10, 1000)

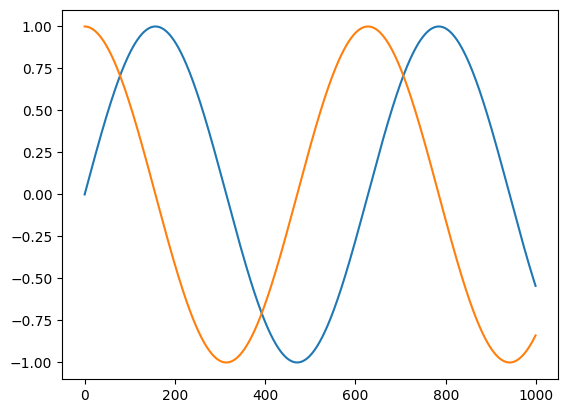
plt.plot(jnp.sin(t))
plt.plot(vmap(grad(jnp.sin))(t))

[<matplotlib.lines.Line2D at 0x7fae4edc7370>]

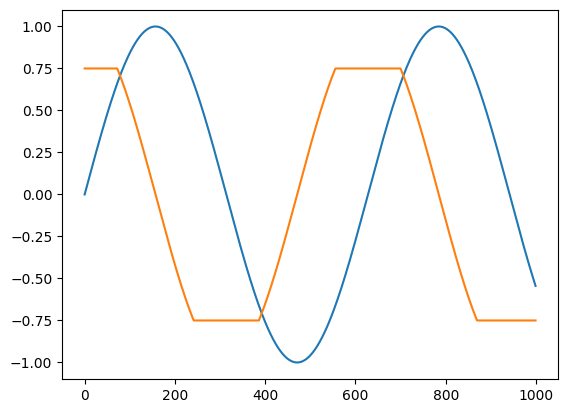
def clip_sin(x):
  x = clip_gradient(-0.75, 0.75, x)
  return jnp.sin(x)

plt.plot(clip_sin(t))
plt.plot(vmap(grad(clip_sin))(t))

[<matplotlib.lines.Line2D at 0x7fae4eccbdf0>]

示例：Python 调试

另一个受开发工作流程而不是数值问题驱动的应用是在反向模式自动微分的反向传播中设置一个 pdb 调试器跟踪。

在尝试追踪 nan 运行时错误的来源，或者只是仔细检查正在传播的余切（梯度）值时，在与主计算中的特定点相对应的反向传播中的某个点插入一个调试器会很有用。你可以使用 jax.custom_vjp() 来实现这一点。

我们将把一个例子留到下一节。

示例：迭代实现的隐式函数微分

这个例子在数学的细枝末节上深入探讨了！

另一个应用 jax.custom_vjp() 的地方是反向模式微分，这些函数可以通过 JAX 进行转换（通过 jax.jit()，jax.vmap()，…），但由于某些原因无法有效地进行 JAX 微分，可能是因为它们涉及 jax.lax.while_loop()。（不可能生成一个能够有效地计算 XLA HLO While 循环的反向模式导数的 XLA HLO 程序，因为这将需要一个具有无限内存使用的程序，而这在 XLA HLO 中无法表达，至少在没有通过进/出馈进行“副作用”交互的情况下无法表达。）

例如，考虑这个 fixed_point 例程，它通过在 while_loop 中迭代地应用一个函数来计算不动点

from jax.lax import while_loop

def fixed_point(f, a, x_guess):
  def cond_fun(carry):
    x_prev, x = carry
    return jnp.abs(x_prev - x) > 1e-6

  def body_fun(carry):
    _, x = carry
    return x, f(a, x)

  _, x_star = while_loop(cond_fun, body_fun, (x_guess, f(a, x_guess)))
  return x_star

这是一个迭代过程，用于通过迭代 \(x_{t+1} = f(a, x_t)\) 直到 \(x_{t+1}\) 足够接近 \(x_t\) 来数值求解方程 \(x = f(a, x)\) 以得到 \(x\)。结果 \(x^*\) 取决于参数 \(a\)，因此我们可以认为存在一个由方程 \(x = f(a, x)\) 隐式定义的函数 \(a \mapsto x^*(a)\)。

我们可以使用 fixed_point 来运行迭代过程直到收敛，例如运行牛顿法来计算平方根，同时只执行加法、乘法和除法

def newton_sqrt(a):
  update = lambda a, x: 0.5 * (x + a / x)
  return fixed_point(update, a, a)

print(newton_sqrt(2.))

1.4142135

我们也可以对函数进行 jax.vmap() 或 jax.jit() 转换

print(jit(vmap(newton_sqrt))(jnp.array([1., 2., 3., 4.])))

[1.        1.4142135 1.7320509 2.       ]

由于 while_loop 的存在，我们无法应用反向模式自动微分，但事实证明我们也不希望这样做：与其对 fixed_point 的实现及其所有迭代进行微分，我们可以利用数学结构来做一些内存效率更高的事情（在本例中，FLOP 效率也更高！）。相反，我们可以使用隐函数定理 [Bertsekas’s Nonlinear Programming 第 2 版，命题 A.25]，它保证（在某些条件下）我们即将使用的数学对象的 存在性。本质上，我们对解进行线性化，并迭代地求解这些线性方程，以计算我们想要的导数。

再次考虑方程 \(x = f(a, x)\) 和函数 \(x^*\)。我们希望评估向量-雅可比乘积，例如 \(v^\mathsf{T} \mapsto v^\mathsf{T} \partial x^*(a_0)\)。

至少在我们要微分点的 \(a_0\) 周围的开邻域中，让我们假设方程 \(x^*(a) = f(a, x^*(a))\) 对所有 \(a\) 都成立。由于两边作为 \(a\) 的函数相等，因此它们的导数也必须相等，因此让我们对两边进行微分

\(\qquad \partial x^*(a) = \partial_0 f(a, x^*(a)) + \partial_1 f(a, x^*(a)) \partial x^*(a)\).

设 \(A = \partial_1 f(a_0, x^*(a_0))\) 且 \(B = \partial_0 f(a_0, x^*(a_0))\)，我们可以将我们想要得到的量更简单地写成

\(\qquad \partial x^*(a_0) = B + A \partial x^*(a_0)\),

或者，通过重新排列，

\(\qquad \partial x^*(a_0) = (I - A)^{-1} B\).

这意味着我们可以评估向量-雅可比乘积，例如

\(\qquad v^\mathsf{T} \partial x^*(a_0) = v^\mathsf{T} (I - A)^{-1} B = w^\mathsf{T} B\),

其中 \(w^\mathsf{T} = v^\mathsf{T} (I - A)^{-1}\)，或者等效地 \(w^\mathsf{T} = v^\mathsf{T} + w^\mathsf{T} A\)，或者等效地 \(w^\mathsf{T}\) 是映射 \(u^\mathsf{T} \mapsto v^\mathsf{T} + u^\mathsf{T} A\) 的不动点。最后一个表述为我们提供了一种用对 fixed_point 的调用来编写 fixed_point 的 VJP 的方法！此外，在将 \(A\) 和 \(B\) 扩展回来之后，你可以得出结论，你只需要在 \((a_0, x^*(a_0))\) 处评估 \(f\) 的 VJP。

以下是重点

@partial(custom_vjp, nondiff_argnums=(0,))
def fixed_point(f, a, x_guess):
  def cond_fun(carry):
    x_prev, x = carry
    return jnp.abs(x_prev - x) > 1e-6

  def body_fun(carry):
    _, x = carry
    return x, f(a, x)

  _, x_star = while_loop(cond_fun, body_fun, (x_guess, f(a, x_guess)))
  return x_star

def fixed_point_fwd(f, a, x_init):
  x_star = fixed_point(f, a, x_init)
  return x_star, (a, x_star)

def fixed_point_rev(f, res, x_star_bar):
  a, x_star = res
  _, vjp_a = vjp(lambda a: f(a, x_star), a)
  a_bar, = vjp_a(fixed_point(partial(rev_iter, f),
                             (a, x_star, x_star_bar),
                             x_star_bar))
  return a_bar, jnp.zeros_like(x_star)
  
def rev_iter(f, packed, u):
  a, x_star, x_star_bar = packed
  _, vjp_x = vjp(lambda x: f(a, x), x_star)
  return x_star_bar + vjp_x(u)[0]

fixed_point.defvjp(fixed_point_fwd, fixed_point_rev)

print(newton_sqrt(2.))

1.4142135

print(grad(newton_sqrt)(2.))
print(grad(grad(newton_sqrt))(2.))

0.35355338
-0.088388346

我们可以通过微分 jnp.sqrt() 来检查我们的答案，它使用了一种完全不同的实现。

print(grad(jnp.sqrt)(2.))
print(grad(grad(jnp.sqrt))(2.))

0.35355338
-0.08838835

这种方法的一个限制是参数 f 不能封闭任何与微分相关的值。也就是说，您可能会注意到我们将参数 a 在 fixed_point 的参数列表中保持显式。对于这种用例，请考虑使用低级原语 lax.custom_root，它允许使用自定义求根函数在封闭变量中进行求导。

jax.custom_jvp 和 jax.custom_vjp API 的基本用法

使用 jax.custom_jvp 来定义正向模式（以及间接的反向模式）规则

以下是一个使用 jax.custom_jvp() 的规范基本示例，其中注释使用 类似 Haskell 的类型签名

# f :: a -> b
@custom_jvp
def f(x):
  return jnp.sin(x)

# f_jvp :: (a, T a) -> (b, T b)
def f_jvp(primals, tangents):
  x, = primals
  t, = tangents
  return f(x), jnp.cos(x) * t

f.defjvp(f_jvp)

<function __main__.f_jvp(primals, tangents)>

print(f(3.))

y, y_dot = jvp(f, (3.,), (1.,))
print(y)
print(y_dot)

0.14112
0.14112
-0.9899925

换句话说，我们从一个原始函数 f 开始，它接受类型为 a 的输入并产生类型为 b 的输出。我们将其与一个 JVP 规则函数 f_jvp 关联起来，该函数接受一对输入，分别代表类型为 a 的原始输入和类型为 T a 的相应切线输入，并产生一对输出，分别代表类型为 b 的原始输出和类型为 T b 的切线输出。切线输出应该是切线输入的线性函数。

您还可以使用 f.defjvp 作为装饰器，如下所示：

@custom_jvp
def f(x):
  ...

@f.defjvp
def f_jvp(primals, tangents):
  ...

即使我们只定义了 JVP 规则，而没有定义 VJP 规则，我们也可以对 f 使用正向和反向模式微分。JAX 会自动转置我们自定义 JVP 规则中对切线值的线性计算，以与我们手动编写规则一样高效地计算 VJP。

print(grad(f)(3.))
print(grad(grad(f))(3.))

-0.9899925
-0.14112

为了使自动转置工作，JVP 规则的输出切线必须作为输入切线的函数是线性的。否则会引发转置错误。

多个参数的工作方式如下

@custom_jvp
def f(x, y):
  return x ** 2 * y

@f.defjvp
def f_jvp(primals, tangents):
  x, y = primals
  x_dot, y_dot = tangents
  primal_out = f(x, y)
  tangent_out = 2 * x * y * x_dot + x ** 2 * y_dot
  return primal_out, tangent_out

print(grad(f)(2., 3.))

12.0

defjvps 便利包装器允许我们分别为每个参数定义一个 JVP，并且结果分别计算然后累加。

@custom_jvp
def f(x):
  return jnp.sin(x)

f.defjvps(lambda t, ans, x: jnp.cos(x) * t)

print(grad(f)(3.))

-0.9899925

这是一个具有多个参数的 defjvps 示例。

@custom_jvp
def f(x, y):
  return x ** 2 * y

f.defjvps(lambda x_dot, primal_out, x, y: 2 * x * y * x_dot,
          lambda y_dot, primal_out, x, y: x ** 2 * y_dot)

print(grad(f)(2., 3.))
print(grad(f, 0)(2., 3.))  # same as above
print(grad(f, 1)(2., 3.))

12.0
12.0
4.0

作为一种简写方式，在 defjvps 中，您可以传递一个 None 值来指示特定参数的 JVP 为零。

@custom_jvp
def f(x, y):
  return x ** 2 * y

f.defjvps(lambda x_dot, primal_out, x, y: 2 * x * y * x_dot,
          None)

print(grad(f)(2., 3.))
print(grad(f, 0)(2., 3.))  # same as above
print(grad(f, 1)(2., 3.))

12.0
12.0
0.0

使用关键字参数调用 jax.custom_jvp() 函数，或使用默认参数编写 jax.custom_jvp() 函数定义都是允许的，只要它们可以根据标准库 inspect.signature 机制检索到的函数签名明确映射到位置参数。

当您不执行微分时，函数 f 的调用方式与没有被 jax.custom_jvp() 装饰一样。

@custom_jvp
def f(x):
  print('called f!')  # a harmless side-effect
  return jnp.sin(x)

@f.defjvp
def f_jvp(primals, tangents):
  print('called f_jvp!')  # a harmless side-effect
  x, = primals
  t, = tangents
  return f(x), jnp.cos(x) * t

print(f(3.))

called f!
0.14112

print(vmap(f)(jnp.arange(3.)))
print(jit(f)(3.))

called f!
[0.         0.84147096 0.9092974 ]
called f!
0.14112

自定义 JVP 规则在微分过程中被调用，无论是正向还是反向。

y, y_dot = jvp(f, (3.,), (1.,))
print(y_dot)

called f_jvp!
called f!
-0.9899925

print(grad(f)(3.))

called f_jvp!
called f!
-0.9899925

请注意，f_jvp 调用 f 来计算原始输出。在高阶微分的上下文中，只有当规则调用原始 f 来计算原始输出时，微分变换的每次应用才会使用自定义 JVP 规则。（这代表了一种基本权衡，我们不能在规则中使用 f 评估的中间值 *并同时* 使规则适用于所有阶高阶微分。）

grad(grad(f))(3.)

called f_jvp!
called f_jvp!
called f!

Array(-0.14112, dtype=float32, weak_type=True)

您可以在 jax.custom_jvp() 中使用 Python 控制流。

@custom_jvp
def f(x):
  if x > 0:
    return jnp.sin(x)
  else:
    return jnp.cos(x)

@f.defjvp
def f_jvp(primals, tangents):
  x, = primals
  x_dot, = tangents
  ans = f(x)
  if x > 0:
    return ans, 2 * x_dot
  else:
    return ans, 3 * x_dot

print(grad(f)(1.))
print(grad(f)(-1.))

2.0
3.0

使用 jax.custom_vjp 来定义自定义反向模式专用规则

虽然 jax.custom_jvp() 足以控制正向和通过 JAX 的自动转置的反向模式微分行为，但在某些情况下，我们可能希望直接控制 VJP 规则，例如在上面介绍的最后两个示例问题中。我们可以使用 jax.custom_vjp() 来做到这一点。

from jax import custom_vjp

# f :: a -> b
@custom_vjp
def f(x):
  return jnp.sin(x)

# f_fwd :: a -> (b, c)
def f_fwd(x):
  return f(x), jnp.cos(x)

# f_bwd :: (c, CT b) -> CT a
def f_bwd(cos_x, y_bar):
  return (cos_x * y_bar,)

f.defvjp(f_fwd, f_bwd)

print(f(3.))
print(grad(f)(3.))

0.14112
-0.9899925

换句话说，我们再次从一个原始函数 f 开始，它接受类型为 a 的输入并产生类型为 b 的输出。我们将其与两个函数 f_fwd 和 f_bwd 关联起来，它们分别描述了如何执行反向模式自动微分的正向和反向传递。

函数 f_fwd 描述了正向传递，不仅是原始计算，还包括哪些值要保存以供反向传递使用。它的输入签名与原始函数 f 一样，因为它接受类型为 a 的原始输入。但作为输出，它产生了一对，其中第一个元素是原始输出 b，第二个元素是任何类型为 c 的“残余”数据，将被存储以供反向传递使用。（这个第二个输出类似于 PyTorch 的 save_for_backward 机制。）

函数 f_bwd 描述了反向传递。它接受两个输入，其中第一个是 f_fwd 生成的类型为 c 的残余数据，第二个是对应于原始函数输出的类型为 CT b 的输出余切。它产生类型为 CT a 的输出，表示对应于原始函数输入的余切。特别是，f_bwd 的输出必须是长度等于原始函数参数数量的序列（例如元组）。

因此，多个参数的工作方式如下

@custom_vjp
def f(x, y):
  return jnp.sin(x) * y

def f_fwd(x, y):
  return f(x, y), (jnp.cos(x), jnp.sin(x), y)

def f_bwd(res, g):
  cos_x, sin_x, y = res
  return (cos_x * g * y, sin_x * g)

f.defvjp(f_fwd, f_bwd)

print(grad(f)(2., 3.))

-1.2484405

使用关键字参数调用 jax.custom_vjp() 函数，或使用默认参数编写 jax.custom_vjp() 函数定义都是允许的，只要它们可以根据标准库 inspect.signature 机制检索到的函数签名明确映射到位置参数。

与 jax.custom_jvp() 一样，如果未应用微分，则不会调用由 f_fwd 和 f_bwd 组成的自定义 VJP 规则。如果函数被评估，或者使用 jax.jit()、jax.vmap() 或其他非微分变换进行转换，则只调用 f。

@custom_vjp
def f(x):
  print("called f!")
  return jnp.sin(x)

def f_fwd(x):
  print("called f_fwd!")
  return f(x), jnp.cos(x)

def f_bwd(cos_x, y_bar):
  print("called f_bwd!")
  return (cos_x * y_bar,)

f.defvjp(f_fwd, f_bwd)

print(f(3.))

called f!
0.14112

print(grad(f)(3.))

called f_fwd!
called f!
called f_bwd!
-0.9899925

y, f_vjp = vjp(f, 3.)
print(y)

called f_fwd!
called f!
0.14112

print(f_vjp(1.))

called f_bwd!
(Array(-0.9899925, dtype=float32, weak_type=True),)

无法对 jax.custom_vjp() 函数使用正向模式自动微分，并将引发错误。

from jax import jvp

try:
  jvp(f, (3.,), (1.,))
except TypeError as e:
  print('ERROR! {}'.format(e))

called f_fwd!
called f!
ERROR! can't apply forward-mode autodiff (jvp) to a custom_vjp function.

如果您想使用正向和反向模式，请改用 jax.custom_jvp()。

我们可以将 jax.custom_vjp() 与 pdb 一起使用，以便在反向传递中插入调试器跟踪。

import pdb

@custom_vjp
def debug(x):
  return x  # acts like identity

def debug_fwd(x):
  return x, x

def debug_bwd(x, g):
  import pdb; pdb.set_trace()
  return g

debug.defvjp(debug_fwd, debug_bwd)

def foo(x):
  y = x ** 2
  y = debug(y)  # insert pdb in corresponding backward pass step
  return jnp.sin(y)

jax.grad(foo)(3.)

> <ipython-input-113-b19a2dc1abf7>(12)debug_bwd()
-> return g
(Pdb) p x
Array(9., dtype=float32)
(Pdb) p g
Array(-0.91113025, dtype=float32)
(Pdb) q

更多功能和细节

使用 list / tuple / dict 容器（和其他 pytree）

您应该期望标准 Python 容器（如列表、元组、命名元组和字典）以及它们的嵌套版本可以正常工作。一般来说，任何 pytree 都是允许的，只要它们根据类型约束一致。

以下是一个使用 jax.custom_jvp() 的人为示例。

from collections import namedtuple
Point = namedtuple("Point", ["x", "y"])

@custom_jvp
def f(pt):
  x, y = pt.x, pt.y
  return {'a': x ** 2,
          'b': (jnp.sin(x), jnp.cos(y))}

@f.defjvp
def f_jvp(primals, tangents):
  pt, = primals
  pt_dot, =  tangents
  ans = f(pt)
  ans_dot = {'a': 2 * pt.x * pt_dot.x,
             'b': (jnp.cos(pt.x) * pt_dot.x, -jnp.sin(pt.y) * pt_dot.y)}
  return ans, ans_dot

def fun(pt):
  dct = f(pt)
  return dct['a'] + dct['b'][0]

pt = Point(1., 2.)

print(f(pt))

{'a': 1.0, 'b': (Array(0.84147096, dtype=float32, weak_type=True), Array(-0.41614684, dtype=float32, weak_type=True))}

print(grad(fun)(pt))

Point(x=Array(2.5403023, dtype=float32, weak_type=True), y=Array(0., dtype=float32, weak_type=True))

以及使用 jax.custom_vjp() 的类似人为示例。

@custom_vjp
def f(pt):
  x, y = pt.x, pt.y
  return {'a': x ** 2,
          'b': (jnp.sin(x), jnp.cos(y))}

def f_fwd(pt):
  return f(pt), pt

def f_bwd(pt, g):
  a_bar, (b0_bar, b1_bar) = g['a'], g['b']
  x_bar = 2 * pt.x * a_bar + jnp.cos(pt.x) * b0_bar
  y_bar = -jnp.sin(pt.y) * b1_bar
  return (Point(x_bar, y_bar),)

f.defvjp(f_fwd, f_bwd)

def fun(pt):
  dct = f(pt)
  return dct['a'] + dct['b'][0]

pt = Point(1., 2.)

print(f(pt))

{'a': 1.0, 'b': (Array(0.84147096, dtype=float32, weak_type=True), Array(-0.41614684, dtype=float32, weak_type=True))}

print(grad(fun)(pt))

Point(x=Array(2.5403023, dtype=float32, weak_type=True), y=Array(-0., dtype=float32, weak_type=True))

处理不可微分参数

一些用例（如最后一个示例问题）需要将不可微分参数（如函数值参数）传递给具有自定义微分规则的函数，并将这些参数也传递给规则本身。在 fixed_point 的情况下，函数参数 f 就是这样的不可微分参数。类似的情况也发生在 jax.experimental.odeint 中。

jax.custom_jvp 与 nondiff_argnums

使用可选的 nondiff_argnums 参数到 jax.custom_jvp() 来指示像这样的参数。以下是用 jax.custom_jvp() 的例子

from functools import partial

@partial(custom_jvp, nondiff_argnums=(0,))
def app(f, x):
  return f(x)

@app.defjvp
def app_jvp(f, primals, tangents):
  x, = primals
  x_dot, = tangents
  return f(x), 2. * x_dot

print(app(lambda x: x ** 3, 3.))

27.0

print(grad(app, 1)(lambda x: x ** 3, 3.))

2.0

注意这里有个陷阱：无论这些参数出现在参数列表中的哪个位置，它们都会被放置在相应 JVP 规则签名的开头。这里还有另一个例子

@partial(custom_jvp, nondiff_argnums=(0, 2))
def app2(f, x, g):
  return f(g((x)))

@app2.defjvp
def app2_jvp(f, g, primals, tangents):
  x, = primals
  x_dot, = tangents
  return f(g(x)), 3. * x_dot

print(app2(lambda x: x ** 3, 3., lambda y: 5 * y))

3375.0

print(grad(app2, 1)(lambda x: x ** 3, 3., lambda y: 5 * y))

3.0

jax.custom_vjp 与 nondiff_argnums

对于 jax.custom_vjp() 也存在类似的选择，并且同样地，惯例是将不可微分参数作为 _bwd 规则的第一个参数传递，无论它们出现在原始函数签名的哪个位置。_fwd 规则的签名保持不变 - 它与原始函数的签名相同。这里有一个例子

@partial(custom_vjp, nondiff_argnums=(0,))
def app(f, x):
  return f(x)

def app_fwd(f, x):
  return f(x), x

def app_bwd(f, x, g):
  return (5 * g,)

app.defvjp(app_fwd, app_bwd)

print(app(lambda x: x ** 2, 4.))

16.0

print(grad(app, 1)(lambda x: x ** 2, 4.))

5.0

请参考上面的 fixed_point 获取另一个用法示例。

您不需要 nondiff_argnums 用于数组值参数，例如，具有整数数据类型的参数。相反，nondiff_argnums 应该只用于不对应于 JAX 类型（本质上不对应于数组类型）的参数值，例如 Python 可调用对象或字符串。如果 JAX 检测到由 nondiff_argnums 指示的参数包含 JAX Tracer，则会引发错误。上面的 clip_gradient 函数是一个不使用 nondiff_argnums 用于整数数据类型数组参数的良好示例。

下一步

还有许多其他自动微分技巧和功能。本教程中未涵盖但值得探讨的主题包括

• Gauss-Newton 向量积，一次线性化

• 自定义 VJP 和 JVP

• 固定点处的有效导数

• 使用随机 Hessian-向量积估计 Hessian 的迹

• 仅使用反向模式自动微分进行正向模式自动微分

• 相对于自定义数据类型求导数

• 检查点（用于高效反向模式的二项式检查点，而不是模型快照）

• 使用雅可比预累积优化 VJP